To find the derivative of \(\sin(x)\) we need know that \(\lim\limits_{x \to 0}\frac{\sin x}{x} = 1\). The limit itself is quite trivial, but I always forget how you start.
The key is similar triangles and the so called “squeeze” theorem for limits:
Consider the sector ABD of the unit circle shown below
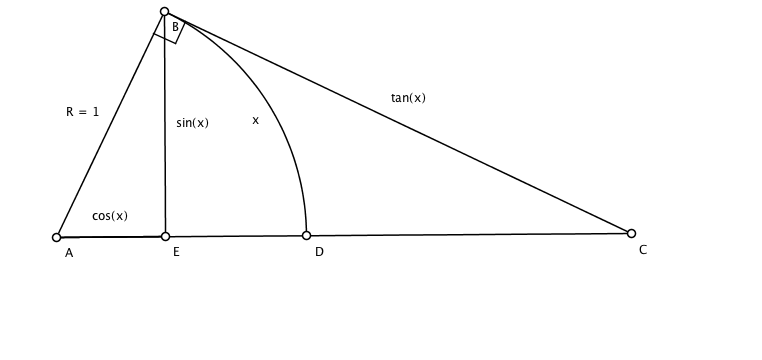AB and AD are radii (and since this is the unit circle the radius is 1); \(x\) is the arc of the unit circle subtended (?) by AB and AD; by definition of sine and cosine, \(\sin(x) = BE\) and \(\cos(x) = AE\)
We need to make the following assumptions:
- Two triangles are similar if two of their angles are congruent (AA or AAA postulate) (And we’re going to assume we know what similar means and what are the consequences of that.)
- Given two “shapes” (or more abstractly, sets) A and B, if for every point in shape A the point is also in shape B (or in the language of sets \( A \subseteq B\)) then area of A is less than or equal to the area of B. (In other words if shape A is completely within shape B then the area of A will be less than or equal to the area of B) Of course this assumes that we know what area is (i.e. that it is well defined.) That is not trivial, but we’ll assume we know what were talking about.)To be a bit more specific our notion of area, \(\mu()\), of a “shape” (i.e. a set) must satisfy the following:given sets \(A\) and \(B\), if the areas \(\mu(A)\) and \(\mu(B)\) are defined and \(A \subseteq B\) then \(\mu(A) \le \mu(B)\)
- By inspection and #2: \( \text{Area of} \bigtriangleup ABE \le \text{Area of sector } ABD \le \text{Area of} \bigtriangleup ABC\).
The first thing to note is that \(\bigtriangleup ABE \sim \bigtriangleup BCE\) and therefore
\[
\displaystyle \frac{AB}{AE}=\frac{BC}{BE}
\]
Substituting our known lengths, we have
\[
\displaystyle \frac{1}{\cos(x)} = \frac{BC}{\sin(x)}
\]
Therefore
\[
\displaystyle BC = \frac{\sin(x)}{\cos(x)}=\tan(x)
\]
Having expressed all lengths in terms of \(x\), we can compute the areas of the triangles and sectors:
\[
\begin{align}
\text{Area of } \bigtriangleup \text{ABE} \quad & \le & \text{Area of sector } x \quad & \le & \text{Area of } \bigtriangleup \text{ABC} \\
\frac{1}{2} \times \cos(x) \times \sin(x) \quad & \le & \pi 1^2\times \frac{x}{2\pi} \quad & \le & \frac{1}{2} \times 1 \times \tan(x) \\
\frac{\sin(x)\cos(x)}{2} \quad &\le &\frac{x}{2} \quad & \le & \frac{\tan{x}}{2} \\
\cos(x) \quad & \le & \frac{x}{\sin(x)} \quad & \le & \frac{1}{\cos(x)}
\end{align}
\]
We can then reverse the inequalities by taking the reciprocals:
\[
\displaystyle \frac{1}{\cos(x)} \ge \frac{\sin(x)}{x} \ge \cos(x)
\]
Now we can let \( x \to 0\). The limits on either side of the inequalities are \( \displaystyle \lim\limits_{x\to 0} \frac{1}{\cos(x)}=\lim\limits_{x\to 0} \cos(x) = 1 \) and thus by the “squeeze” theorem:
\[
\displaystyle \lim\limits_{x \to 0^{+}} \frac{\sin{x}}{x}=1
\]
We can only take the limit from the positive side because of how we have set up the inequalities. (The inequalities are the areas of the inscribed triangle, the sector and the circumscribed triangle.) Thus a “negative” side or area makes no sense. But this is easily rectified.For the limit from the other side:
\[
\displaystyle \lim\limits_{x\to 0^{-}} \frac{\sin(x)}{x}=\lim\limits_{x \to 0^{+}}\frac{\sin(-x)}{-x}=\lim\limits_{x \to 0^{+}}\frac{-\sin(x)}{-x}=\lim\limits_{x \to 0^{+}}\frac{\sin(x)}{x}=1
\]
Since the limits from each side are defined and equal, the limit itself is defined.
QED
Notes:
- Many proofs I see use the assumption that BE < BD < BC, rather than the size of the triangles. I find this a little but non intuitive. I can maybeaccept the assumption that BE < BC. Using this assumption means that one has already proven or taken for granted that the shortest distance from a point (B) to a line (AC) is the segment through the point which is perpendicular to the line. Any other segment from the point to the line must necessarily be greater. Although this is true, it is not so immediately obvious. What I believe is in no way obvious though is that the length of the arc BD is something between the lengths BE and BC.On the other hand it seems much more obvious to me that if every point in set X is also in set Y (but perhaps not the other way around) then the “area” of Y must be at least as big as the area of X ( \( \mu(X) \leq \mu(Y) \) ). If you can accept that there is some sort of notion of what an area is for the simple shapes of triangles and sectors, then I believe this assumption to be much more obvious.
